2023年8月18日に投稿したケルヴィン男爵さんの積分器ですが掛け算割り算にも使えます。
今迄二回ほどアナログコンピュータで足し算引き算をする方法を紹介してきました。
もっとたくさんのやり方があるので後日またどんどん紹介しますが、足し算引き算ばかり一気に紹介していると誰にも読んでいただけなくなってしまうので、ここで掛け算割り算の紹介をします。
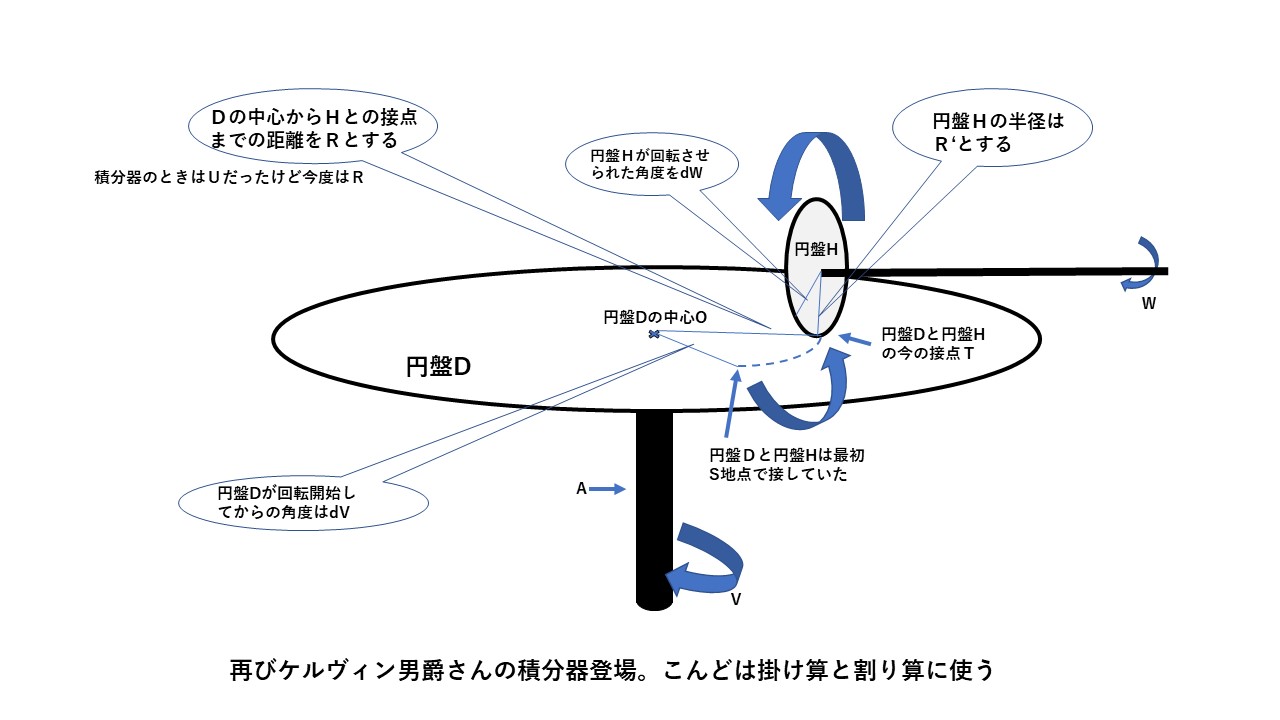
画像は見た目そっくりですが、少しは変えないと面白くないので、今回掛け算割り算を紹介するにあたり、水平円盤Dの中心から垂直円盤Hが接触する点までの距離をこんどはRとします。
8月18日のときはUとしました。
同じものを違う記号で表すと混乱するでしょう。(こういう節操のないことをしても混乱しない人はすごいなと思います)
垂直円盤Hの半径をR’とします。
水平円盤Dが回転する角速度をωとします。 なんでωとするかと言いますと、電気や電子の技術者なら想像がつくように電気の世界でも角速度はωで表すからです。
電気電子の関係者は角速度ωを2×π×周波数で扱っています。
周波数は「1秒間に何周するか」ですよね。
垂直円盤Hの角速度をω’とすればこれは ω’=(R/R’)×ωの関係になります。
円盤D(水平のほう)と円盤H(垂直のほう)の回転角度をそれぞれΘ、Θ’とします。
するとさきほどと同じような形の式Θ’=(R/R’)×Θ。
このメカで変更できるのは円盤Dの中心から円盤Hまでの距離です。
もうひとつは円盤の回転速度です。
これらの要素をオペレータさんが按配することで掛け算割り算をできることがおわかりでしょう。
掛け算割り算にも使えるケルヴィン男爵さんの積分器








コメント
コメント一覧 (1件)
I like this site very much, Its a very nice post to read and
find info.Blog monry