真空管その２

たしか中学生のころに先生から真空管の授業ちゅうに（「真空管の授業」なんて無かったから技術家庭科だったと思いますけど）「２極管より３極管のほうが先に発明された」と聞いてびっくりしました。
だから３極管のほうを先に説明するほうが自然だと思います。
でも教科書をちらほら読んだり、ネットを見たりするとみんな２極管を先に説明していますよね。
３極管のほうが３０年以上いや４０年近く歴史が古いのに。
(申し訳ありません。上の話は私の記憶違いでした。本当は２極管のほうが先でした。
　2023年10月23日　慎んで訂正いたします）
こういうことって他にもありますよね。
算数の積分と微分の関係がそうらしいです。
微分はニュートンさんやライプニッツさんが１６００年代後半から１７００年代初頭にかけて「どっちが先に考え出したのか」を争っていましたけど、積分の話になるとエジプト出身の元関取の力士、大砂嵐関さんが「積分はエジプトが元祖だ」とおっしゃっていました。
相撲と積分との関係は知りませんが、大砂嵐関さんの説によれば昔はナイル川が毎年氾濫していたのだそうです。
（今はアスワンハイダムというのがあって大丈夫らしいです）
ものすごい昔、毎年ナイル川の氾濫が終わったあと（つまり水がひいたあと）肥沃された農地を元の地主に同じ面積ずつ割り振るときに積分計算でちゃんとやっていたのだそうです。
エジプト人力士が（テレビで）言っていたので私は信じています。
でも中国で江南地域（揚子江の南岸地域）を旅したときには「いや積分は中国で発明されたものだ」と言っていたかたもいましたし、韓国人の方々は「積分は韓国で始まったに決まってるよ」と言っていたし、どれが本当なのか私にはわかりません。
どれもみなニュートンさんとライプニッツさん時代より古い話だったので「微分より積分のほうが先だ」という点は共通しています。
とにかく日本の学校で習う順序は微分が先だけど、積分のほうが先に使われていたという説が正しいのなら、多数決で積分が先だと思います。
従って真空管も三極管を先にご説明いたします。
真空管の構造としては２極管のほうが単純です。
２極しかないので３極より単純なのです。
でも３極管の話を先にスタートします。
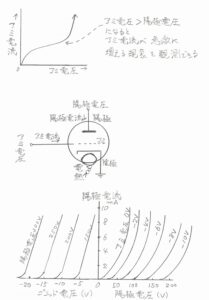
２極管は陰極と陽極が対峙していて片方にしか電子が移動しないのに対して三極管は交流電流が行ったり来たりします。
陰極と陽極の間に網があってこれへの電気の供給をコントロールして、入力の交流振幅よりも出力の交流振幅を揺れ幅を大きくする働きもあります。
こういうのを増幅と言います。　振幅の増幅ですね。
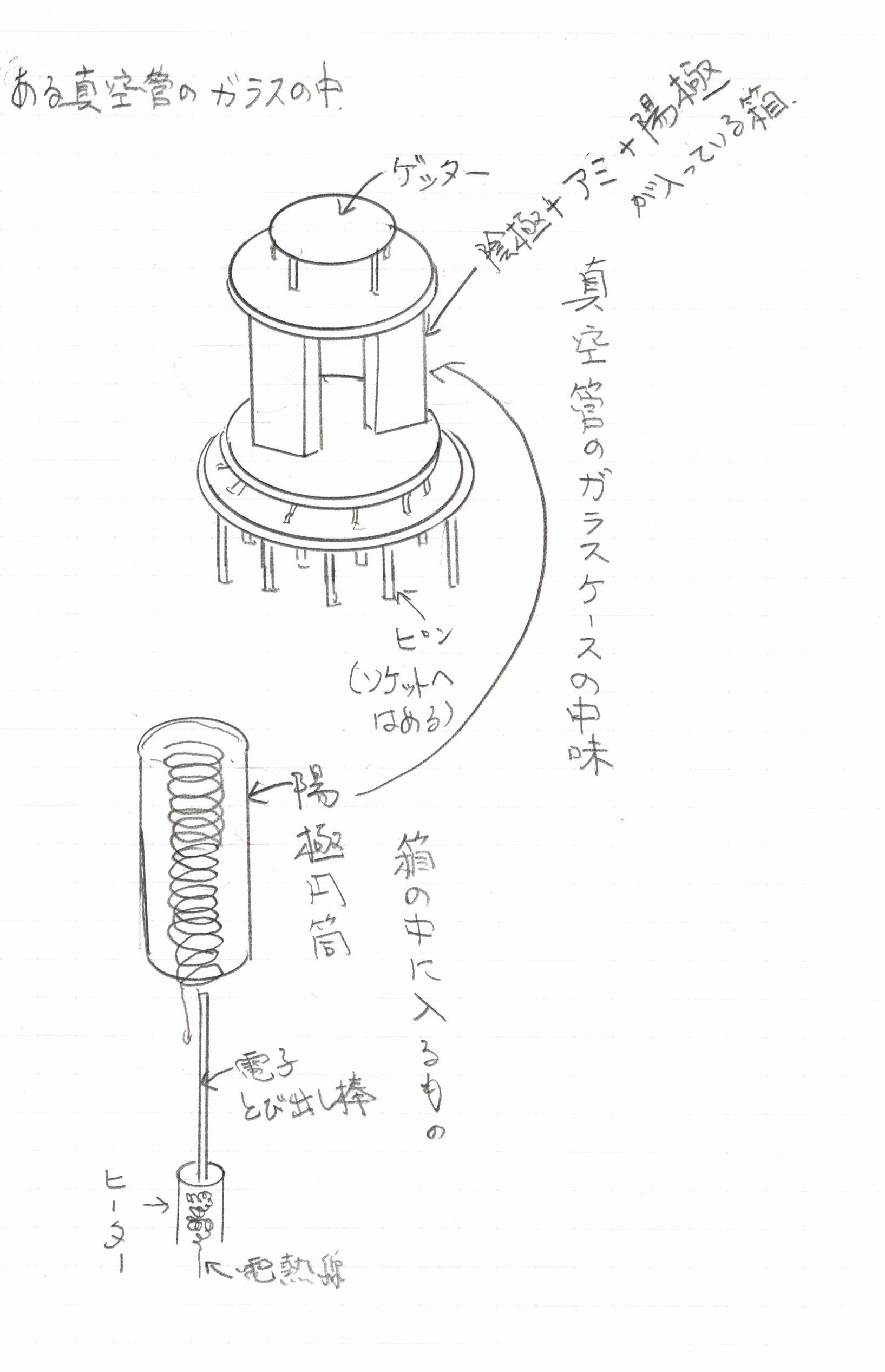
手描きのスケッチは昔の授業で先生が真空管のガラスをはずした教材を持ち込んできたのでノートにスケッチしておいたのを、７０年近くの時空を超えて今、新しい紙に書き写した絵です。
この程度の図なら、どこかに写真があるとは思いますが、ネットで勝手に他人の写真を盗むことは犯罪になります。
だからヘタな絵ですが、これでかんべんしてください。
上側の絵はガラスがはずされて金属の箱が２つ並んでいるだけの絵です。
下の絵は金属の箱の中に陰極と網が入っていたのを取り出したものです。
コイルみたいなのがアミで外側の円筒が陽極です。
このコイルみないな網の真ん中へ棒が挿入されます。
その棒が陰極です。
そして下のほうに、ヒーター電熱線がおさまった円筒があります。
この円筒の中に電熱線が収まっています。
この電熱線に電気を通ると、ヒーターの熱が棒に伝わります。
棒から熱電子がとび出します。
そうして中空にあるコイルみたいなアミの電圧の変化に影響されて外側円筒の陽極へ飛ぶ電子たちはアミを通り抜けるときに振幅に大きく影響が出ます。
もうひとつはこのアミによる電気的制御で熱電子の移動を遮断したり通したりすることもあります。
いわゆるスイッチングですね。
　「まぁそれだけのことですよ」と言ってしまえば身もふたもありません。

ここから本気で細かいことまで説明を始めるとものすごく長い話になります。
大雑把な話で終わらせるつもりですが、それでも数日はかかります。
次回はこの陰極が熱せられて熱電子がアミをどうすり抜けてどういうふうに陽極へたどりつくかを絵で説明します。
そのあと、もっと実用回路として使うときの設計者がどういう計算をするのかを紹介します。
そのあとは２極管の説明をします。
そのあと、４極管など多極管の話。
そして、いままでときどき出てきた不思議な話である「直流増幅器」の説明をします。
ざっと見積もると６日から８日ぐらいかかってしまいます。
３日間で終わらせてしまうつもりでしたが、今迄のアナログ演算器で真空管が持っていた役割をひととおり説明するとなるとどうしても・・・・