アナログコンピュータのプログラミングと言えば微分方程式の話がほとんどですよね。
このブログでは難しい微分方程式は扱いません。(扱えません)
自動制御機械のお仕事をいただいたときにはいろいろやりましたが「ユーチューブで塾の先生が動画で解説しているレベルの数式をアナログコンピュータでプログラミングするとこういう手順になりますよ」という話にします。
そうすれば「なんだ。そういう並びにすれば良いのね」とわかりますよね。
昔のアナログコンピュータの素子ならべの資料をまだ持っているので見たのですけど、すごく実践的なのですよ。
さまざまな調整を入れていて「この式がなんでこういう素子ならびになるの?」と考え込んでしまいました。
小学校のころに算数の問題で最後に約分をしてしまうとバツにする先生がいました。
計算の正確さではなくて考え方がわかっているかどうかを見るということでした。
このブログも式を整理して計算しやすく形を変えるようなことはしません。
「両辺に何々をかけて数式を単純化して・・・」みたいなことはしません。
でも実際のアナログコンピュータプログラミングではそれを徹底してやります。
そうしてパラメータの数を極限まで減らすことがたいせつなのです。
アナログコンピュータは素子を削れるだけ数らないと各素子で発生する「誤差」が積もり積もってしまい計算結果に誤差がたまってしまうのです。
このブログではそういうかっこいいことはしません。
ちゃんと組めるようになってから皆さんで好きなだけチューニングしてください。
では手描きの絵をご覧ください。
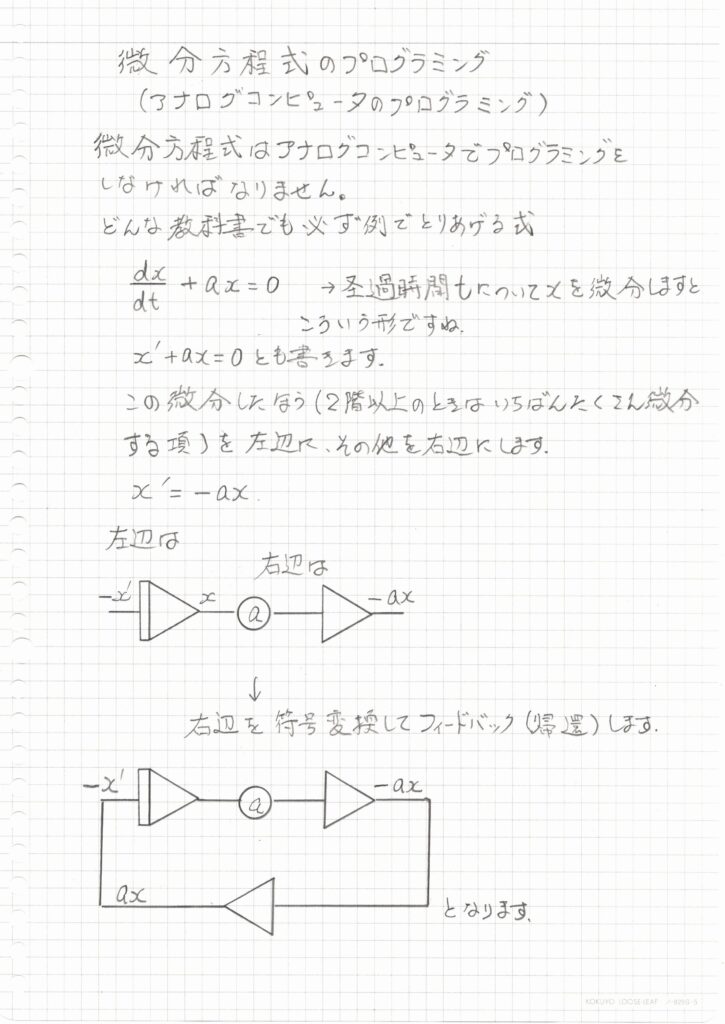
xを経過時間tで微分する。
というときはdx/dt + ax = 0 とか x’ + ax = 0 と書きます。
微分方程式をプログラミングするときの手順はまずいちばんたくさん微分する項(2階微分方程式なら2階の項、3階なら3階の項・・)を左辺に書いて残りを右辺に書きます。
x’ = -ax
というふうに移項するところから始めます。
残りを右辺に書きます。
そして
素子をならべます。
左辺はx’ですから手書き絵のようにまず左辺用に積分器をひとつ書きます。
右辺は、まず係数器を書きます。
丸の中にaですね。
その後ろに符号を逆にする素子をつなぎます。
あっというまに「x’ = -ax」ができました。
符号を戻すために最後を符号逆にする素子をならべておしまいです。
これで完成です。
・・・と言いたいところですが符号変換器が二つあるのは(普通の符号変換と負帰還回路のところへ入れている符号変換器)無駄ですよね。
こういうのをできるだけ排除するほうが精度があがります。
そういう意味でこの符号変換器は2個とも削除したほうが良いです。
符号変換器はプラスとマイナスを反対にするものですから一回で反対になり、二回で元に戻るのですからこれは自明の理としておわかりいただけると思います。
この手描きの絵では「どこで波形を見るのか」を記入し忘れました。
ごめんなさい。
これは二個目の符号変換器の出口ですつまり「ax」と書いた場所につけてください。
符号変換器2個を削除した場合は係数器(〇の中にaと書いた記号)の出力側です。
入力が-xなので式の変形の最終形であるx’ = -ax は実機のアナログコンピュータ上では符号が逆になるのでこうなります。
符号変換器が入る理由はこれがあるからです。
「なんでそうなるの?」と疑問にお思いになるでしょう。
私も不思議でした。(先生に質問しておけばよかった)
これは私の勝手な想像ですが、積分器の回路をシンプルに構成すると符号が逆になってしまいます。このことはこのブログの前のほうをお読みいただければわかると思います。
シンプルではなく必ず符号を戻す回路を付属させていればこの問題は起きません。
でもアナログ回路は部品が増えると誤差がそのぶん増えます。
もっと値段をかければそれを補正する回路をつければ良いのでしょうが、アナログコンピュータ全盛期は「符号が逆なら逆のつもりで読み取れば良いじゃないか」と思ったのかもしれません。
ただし積分器をたくさんつけているうちにわけがわからなくなって符号変換器をつけるようになったのでしょう。
全部直列なら奇数か偶数かを勘定すればわかりますが、並列が混じると場合によってわからなくなりますよね。
たぶんそういう悩みとの格闘のあとだと思います。
今現在のアナログコンピュータがどうなっているのかは知りません。
私の話はあくまでも歴史話ですから「昭和30年代のアナログコンピュータ事情はこうだった」というおつもりでお読みください。
次回は少しパラメータを混じえた例をお示しします。









コメント