「数学力向上チャンネル」というユーチューブをご存知ですか?
私のブログは数学力なんかなくても良いのですが(なんせ私は中卒就職組ですからもともと無い数学力を向上させることにも興味はありません)アナログコンピュータに使われる記号は基本的に数学でつかわれている記号を元にして書く習慣があります。
そこで記号の意味をおさらいするためには例えば「数学力向上チャンネル」がいいなと思いました。
視聴してみたら、中卒就職組の私にもとてもわかりやすいのです。
なんでかなあと思ったら「記号の意味の説明から入ってくださっている」からです。
今回の手描き図や本文で使った記号は「電気特有の記号(たとえばjωみたいな)」のはありませんので、もし「この記号は何んなんだ」とお思いでしたら、あれを視聴なさると良いと思います。
電気電子特有の記号はまた良い解説があるネットを探してご紹介します。本と違ってネットは買わなくても済みますからね。
遅ればせながら・・・お読みくださっている皆様、たいへんご無沙汰いたしました。
このところいろいろなことがありまして半月ぐらいご無沙汰しました。
ひきつづきしばらくはアナログコンピュータの話にお付き合いください。
そのうちちゃんとデジタルコンピュータの話になりますから・・・・。
アナログコンピュータが一番利用されていた分野は微分方程式の解を出すお仕事でした。
しかし微分方程式などという難しい話のその前に「放物線」を計算するお仕事のことを書か
せていただきます。
この話も先輩からの受け売り話です。
あれは私が就職する以前のことでした。
通っていた中学校の用務員さんが海軍ご出身で、フィリピン沖で沈められた戦艦武蔵に乗り組んでいらしたかたでした。
ご存知のかたも多いと思いますが、戦艦武蔵は戦艦大和の同型艦です。(三番館の信濃は航空母艦に改装されていた)
火気管制システムに機械式アナログコンピュータを利用していたそうで(用務員さんは)このあたりのことにはとてもお詳しく新聞広告の紙の裏側をメモ紙にして私達へいろいろとお教えくださった話をここへ記録して遺します。
用務員さんは機械式アナログコンピュータを電子式になおすとどうなるかを個人的に研究なさっていらっしゃったのです。
以下、あのころにお教えいただいた話を受け売りで書かせていただきます。
(昭和30年代に教わった話です)
さていつものとおり、手描きの図をごらんください。
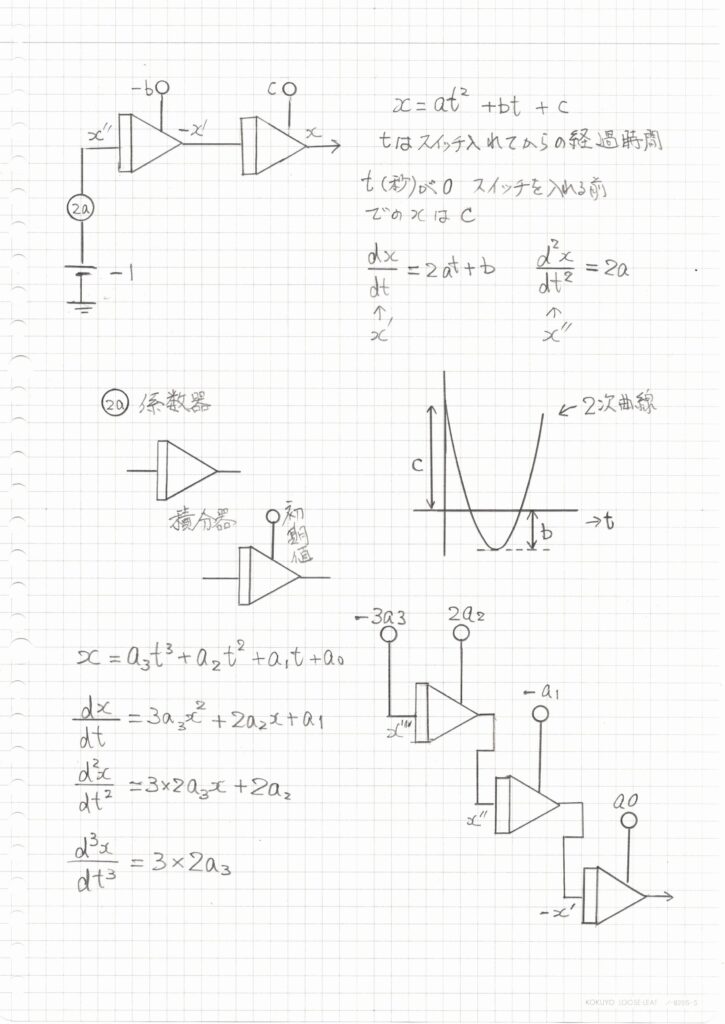
初期値設定端子つきの積分器2台と係数器1台、それに電源をつけます。
これが x = a×t^2 + bt + c
です。
しつこいようですがt^2は「tの2乗」を表します。
ほかに「**2」という表記法もあります。
プログラミング言語では*がひとつだと掛け算の演算、**と2つ並べたら冪数(べきじょう)というのもあります。このブログでも最初のほうで**表記も使っています。
ここではべき乗を表す記号を「^」にします。
では話を先に進めます。
x = a×t^2 + b t+ c
を見て経過時間を表すtが0秒の段階ではx=cです。
この式を微分するとdx/dt=2at+b。
もう一度微分するとd^2x/dt^2=2a。
これを順にブロック線図に記入すると右上の図のようになります。
電源を入れて2aという係数器を入れて積分器を入れて符号反転させます。
符号反転させる理由は当時の積分器は符号反転してしまう回路になっていたので最後にもうひとつ符号反転を入れていました。
・・・はいここで微分の記号を書いてしまいましたが、これも冒頭でご紹介した「数学力向上チャンネル」を視聴してくださるとどなたにももれなくおわかりいただけます。
dx/dtという記号はd/dt×xなんですね。(数学力向上チャンネルより引用)
d/dt×xという記号は「xをtで微分してねという意味ですよ」と先生が動画の中でおっしゃっていますね。
続けてd^2x/dt^2の意味も教えてくださっています。
これはd/dt×d/dt×xのことですよとおっしゃっています。
日本語で言えば「xをまずtで微分して、その答えをもう一回tで微分してねという意味の記号ですよ」とおっしゃっています。
このユーチューブの数学力向上チャンネルの先生が日本語で解説なさっている言葉の順序どおりに積分器をならべてつないでいくこととスケーリング(位どり)と符号が反転したりしなかったりすることに気をつけてあげたらアナログコンピュータのプログラミングは完成します。
デジタルコンピュータのプログラミングでも機械語やアセンブラで組む時は余計な知識は不要で私のような中卒就職組が主に従事していましたが発達の途中から技術に屋上屋を重ねるようにCなどのコンパイラができて誰でも簡単に扱えるようになったと言われるようになったら逆に素朴なやりかたを積み重ねる中卒就職組は駆逐されはじめてしまいました。「中身を抽象化して組み合わせることを得意とする高卒や大学出が自分で簡単にプログラミングする」時代になってしまったからでした。
中卒主力だったプログラマという職業が壊滅してしまいました。
私は不思議なめぐりあわせで定年1年前に退職するまで万年ヒラ社員でプログラマでした。
したがって以下の話は高卒以上のかたにはかえってわかりにくいかもしれませんね。中学を卒業したてのころの自分に戻ってお読みくださるとわかりやすいと思います。
さて二次方程式のプログラミングのお話に戻ります。
一段目の積分器には初期値-bを入れて二段目の積分器には初期値cを与えます。
これでペンレコ(ペン記録器)でt秒の経過にしたがってグラフを描くと二次曲線になります。
グラフを見てください。
t=0秒のときはcの点にいます。
そこから経過時間tに従って二次曲線が描かれます。
「じゃあ3次方程式は?」とお思いでしょうが、それは3つの積分器を直列につなぐことで実現します。
でも二次方程式のつづきに過ぎません。
手描図のいちばん下のほうにある3次方程式とその微分の式と2度微分した式と3度微分した式をご覧ください。
x=a3t^3+a2t^2+a1t+a0
一度微分してdx/dt=3a3x^2+2a2x+a1
二度微分してd^2x/dt^2=3×2a3x+2a2
三度微分してd^3x/dt^3=3×2a3
これらの式の右側をご覧ください
3乗の項のための積分器から順に2度微分用積分器そして三度微分用の積分器とすべて積分器を直列につなぐだけで良いことがわかります。
このやりかたは昔はあまり使えませんでした。
スイッチを入れてからの時刻の経過について微分するのでそれぞれの積分器に与える初期値を変えるたびにクリヤーして最初からやり直す必要があるため、当時の理科の実験ではこういうことにどんくさい私たちの班は何度もやりなおしさせられてたいへんでした。
(今は中学でこういうことはしないそうですね。 昔の中学は生徒がついてくるかどうかなんて考えていなかったみたいです。 でも中卒で就職した私達が大学出の人たちと一緒に仕事をできたのは当時の小学校、中学校のむちゃ振り教育のおかげだったと思います)
そもそも2度微分するだの三度微分するだのそんなことは大学出の人が考えることで私達中卒就職組は言われたことをアナログプログラミングしてスケールを調整してなんとかグラフを描いて(ペンレコーダやオシロスコープへ出力)結果を提出する。
そして大学出の人たちが定数や変数を調整して、また依頼してくるからそれをプログラミングする。
そういうことができる中卒組はとても重宝されました。
私達中卒就職組でさえやっていることが自分では満足にできないのに、役にも立たない理屈をしゃべくるだけの評論家気取りの大学出の人もいました。
どちらが現場でお役にたてたのかは皆さんおわかりですよね。
このブログは屁理屈よりもやり方のご紹介を目的としています。
後世のかたが「へえー。こんなことをしていたんだ」と思ってくださり、何かのお役にたてたら幸いです。
一流の技術者は昔のことを参考にして新たなアイデアを生み出します。
そのときの原料をご提供しているつもりです。
どう参考になさるかはあなた次第です。









コメント
コメント一覧 (2件)
遅ればせながら ブログを拝見しました。
ありがとうございます。
原稿はたくさん書いてあるのですが、サイトへ反映させることをしようとすると用事が入ってしまい、なかなか進みません。
まだアナログコンピュータですが、新年からはデジタルコンピュータの思い出もどんどん入れていきます。
特にもう書籍やネットにはない日本独自の技術であるパラメトロン素子の話などは深い層まで書こうと思います。
電磁気の計算など面倒臭いのですが、いま私が書いておかないとあのころの日本の高かった技術が埋もれてしまうので。
よろしくお願いします。