本日は少し進化しましてふつうの閉回路の計算方法です。
「そんなの中学の理科で習ったよ」とお思いでしょう。
はい団塊世代以上の私たちはたしかに中学で習いました。
私は学歴が代々木中学なので中学までに習ったことだけで生きてきました。
だからオームの法則はよく知っていますが、このような一般的閉回路ではキルヒホッフの法則を使うと言われて最初は何んのことだろう・・・と不安でした。。
またこういう閉じた回路は集中定数回路とも言います。
集中定数回路ではない長い伝送線路の場合は分布定数回路と言います。
念のためキルヒホッフの法則を書いておきます。
第一法則は
電気回路の任意の分岐点について、そこへ流れ込む電流の和は流れ出る電流の和に等しい。
第二法則は、
電気回路の閉じた経路について電位差の和はゼロである。
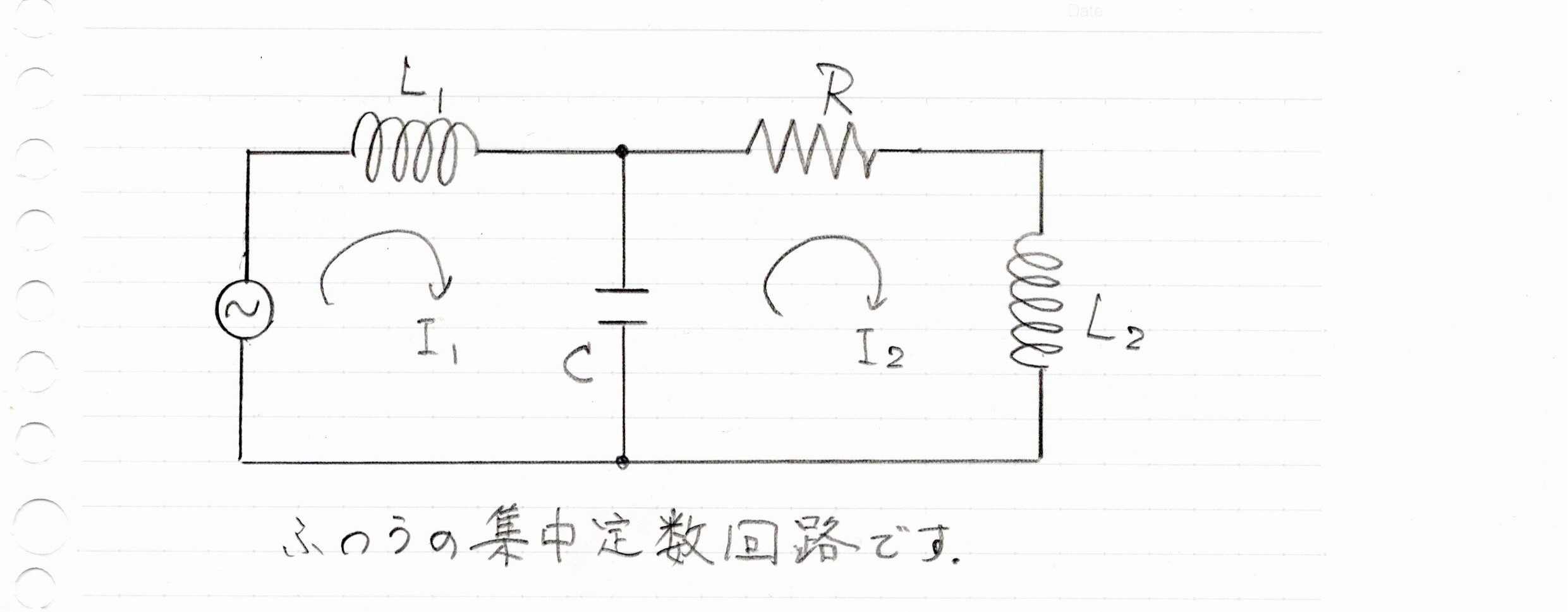
画像でお示しした一般回路例の電圧平衡式は(記号は昨日までの記号と同じ意味です。 お忘れのかたは昨日までの投稿をごらんください)次の式になります。
L1・di1/dt + 1/C∫(i1-i2)dt =e
※ eの記号を図に書き込むことを忘れました。 そのうち入れ替えた画像に差し替えます。
今日のところはご勘弁ください。交流電源の電圧を「e」とします。
もうひとつ
1/C∫(i2-i1)dt + i2R + L2・di2/dt =0
上の式を2度微分してください。
そして下の式へ代入してください。
i2を消去すると次の式になります。
CL1L2・d**3i2/dt**3 + CL1R・d**2i2/dt**2 +(L1+L2)di1/dt +Ri1
=CL2・d**2e/dt**2+RC・de/dt+e
CL1L2・d**3i2/dt**3+CL1R・d**2i2/dt**2+(L1+L2)di2/dt+Ri2=e
※ **2は二乗を**3は3乗をあらわします。 また・は掛け算をあらわします。
「こんな計算式に何んの意味があるんだ?」とお思いでしょう。
この「出力電圧を求める計算」というのが後々基本になります。
いまお話しているのは一般的な電気回路の計算方法です。
電気回路はスイッチを入れてから最初の特別な状況の(過渡現象が現れている間の)計算と安定期に入ったあとの定常計算と違います。
アナログ電子計算機は、この過渡現象が発生しているときに時間の経過とともに現れるいろいろなことを使って経過をしらべて物事の変化を計算することに使います。そのためにはこうした基本的な計算が出てきます。
いまやっているのは、アナログ電子計算機を利用してこの世の現象をシミュレーションするための準備段階なのです。
このまま続けていくとアナログ電子計算機の話になるのですが、まずは電気回路の計算とはこういうものだという話にお付き合いください。
ちなみに、デジタルコンピュータの話になってからも、半導体の歩留まりが悪かったころに東大の大学院生のかたが考案したパラメトロン素子について詳しくお話するときが来ます。(このブログは歴史ブログです)
そのときにやはり電気回路の計算をいやというほどお読みいただきます。
パラメトロン素子の電子計算機のお話のときにパラメトロン素子の詳しいお話をします。
そこへもつながることですので、上のキルヒホッフの法則はお忘れないようにお願いします。









コメント