アナログコンピュータで足し算引き算をするなら（その２）

公立中学校でのアナログ電子計算機教育は令和のいまではすっかりやらなくなってしまったようです。（手軽にデジタルコンピュータが入手できる時代ですからね）
アナログ電子計算機が良いのは微分方程式を解くことですよね。
だからアナログ電子計算機で加減乗除をすることはあまり魅力がありません。

街にある「そろばん教室」はしっかり生き残っているのに計算尺の使い方を教えてくれる教室を見なくなってしまったのも似たような理由でしょう。
ヘンミの計算尺を持っている人もめっきり減りました。
これではいつまでも足し算回路にこだわっていても誰も読んでくれないかもしれません。
すぐにでも微分回路、積分回路に話題を移したい気持ちをこらえてもう少し足し算回路について語ります。
物事には順序があります。
ラグビーの練習ならランニングパスとスクラムフォームとタックルと体当たりの練習。
中国語の練習なら拼音字母の発音と声調の練習。
実につまらない繰り返しでたいていの人はそこでやめてしまいます
飽きっぽい私がラグビーと中国語だけはやめませんでした。
だから足し算回路の話題を続けます。
２回前の投稿（2023年8月27日投稿）のアナログコンピュータで足し算引き算をするなら（その１）の続きをやります。
あの回の記事投稿で抵抗器を組み合わせた足し算回路をまた聞きで紹介しました。
あれを検証しましょう。
入力と出力の計算ソースと計算結果は電圧ですが、電流を媒介にしています。
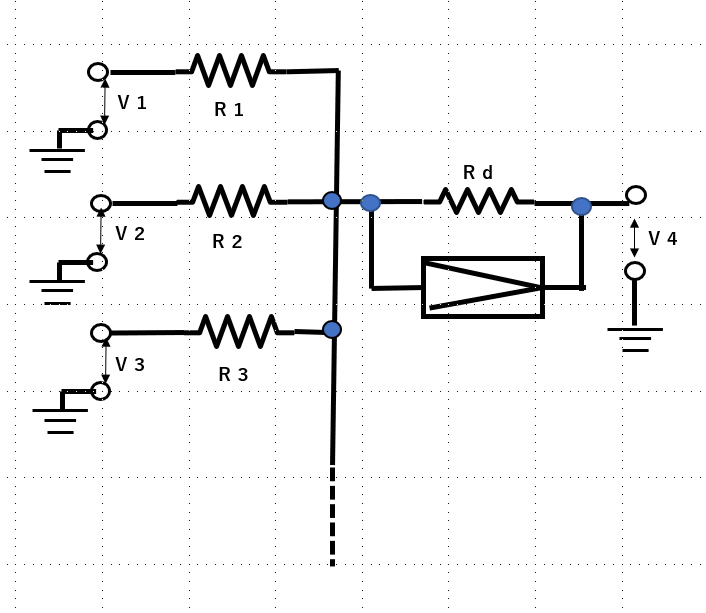
回路図の左側の端子１，２，３、・・・・に電圧V1,V2,V3,・・・をかけて右側の出力電圧（Vd）は左側の全部の電圧を全部の抵抗値で割った数（つまり電流）×｛Ｒd／（Ｒd×左側の全部の抵抗Rjの逆数＋１）｝となります。
この計算はオームの法則の計算式でしかありません。
まとめると・・・・
Ｖｄ＝｛Ｒｄ／（Ｒj＋左側の全Ｒ）｝×左側の全Ｖになります。
右側は足し算結果ですから左側の全電圧より小さくなってしまうとまずいです。
そうならないためにアイキャッチ画像につけたような「足し算増幅器」を使うのがアナログコンピュータの定石なのだそうです。（実は自分でアナログコンピュータを作った経験が無いので「〇〇だそうです」とか「〇〇だと聞いています」という頼りない言い訳をしてしまうことをお許しください。）
　さてあの抵抗器組合せの足し算引き算器の出口の負荷抵抗へ並列に直流増幅器を入れてみたらその問題は解決するということです。
アイキャッチ画像の図はＲ４と並列に直流増幅器をつないだ形です。
この増幅器の増幅度をＡとします。
なんでＡかというと増幅のことを英語でアンプと言いますよね。「ステレオアンプ」なんていう言葉があるくらいですから。
その頭文字がＡだからです。
Ｖd=右側のＶｊ／Ｒjを全部足したもの×（Ａ・Ｒd）／｛（１-Ａ）+Ｒ4×Ｒjの逆数｝
という計算になります。
増幅度Ａがすごく大きいということならＡはＲ4×Ｒjの逆数に等しいとみなせます。
Ｖ4＝－Ｒ4×Ｖj／Ｒjの総和です。
（オームの法則です）
これなら問題無いですよね。
それもそのはずでこの「足し算増幅器」は世界じゅうのアナログコンピュータで使われています。