昭和30年代に小中学生時代を過ごしたいわゆる団塊世代の人はアナログコンピュータをすんなり理解できます。
あのころはソロバンと並んで計算尺も習っていたからでした。
従ってこのブログも計算尺の使い方から入ろうかと思ったこともあります。
でもあえて機械式アナログ計算機の大元になったイギリス國のケルビン男爵さんの積分器から入ってしばらくは機械式とそれを同等に表現する電気の過渡現象をご説明しました。
そして能動素子として昭和初期を彩った真空管をご紹介しました。
いよいよアナログコンピュータのソフトウエアに入ります。
「その前に計算尺は?」とも思いましたがあとでデジタルコンピュータに入るときに計算尺とソロバンの話をしてデジタルコンピュータに切り替わったほうが良いと思い計算尺は後回しにします。
(不評なら電子書籍では変更します。電子書籍ではそれぞれをもっと深堀りします)
アナログもデジタルも本当は計算尺のしくみや使い方を理解していただいてからのほうが良いとは思います。
ソロバンも普通のソロバンではなくて私が上海市で買ってきたような古代中国で関帝廟に祀られている関羽さん(ご存知ないかたは三國志演绎という本を読んでください)が愛用していた昔の中国標準器のソロバンが良いです。
理由は使ってみればわかりますが2のべき乗計算ができるからです。関羽さんすごい)
量子コンピュータやアニーラコンピュータについては自分が扱ったことが無いので書きません。知らないのですから書けません。
知らないと言っても全然知らないわけではないのですが、世の中に出回っている量子コンピュータの本をいくつか読んでみたら、私よりも(量子コンピュータに)無知な人がウソを書いた本をたくさん売っていたりするのを見て他人事ながら恥ずかしくなってしまいましたので、ちょっとさわりに触れる話も含めて一切ここには書きません。
それにしても有名な人があんないい加減な本を書いて値段も2千円ぐらいつけて売っているなんて、いい度胸しているなあと思います。
自分が正しく知っていること、自分が経験したことを書かないとまずいです。
というわけでアナログコンピュータと初期のデジタルコンピュータに絞った話題で書きます。
それでも(自分が正しく理解しているはずでも)間違いはたくさんあると思います。
また数ある説の中の自分が知っている説だけが正しいと思い込んでいることもあります。
そういうのを見つけたらどうかお教えください。
ブログで「このようなご指摘を受けました」と公表させていただきます。
つきましては連絡先としてメールアドレスを正しく記入してくださるようにお願いします。
(ご指摘の意味がよくわからない場合にお問い合わせできるように)
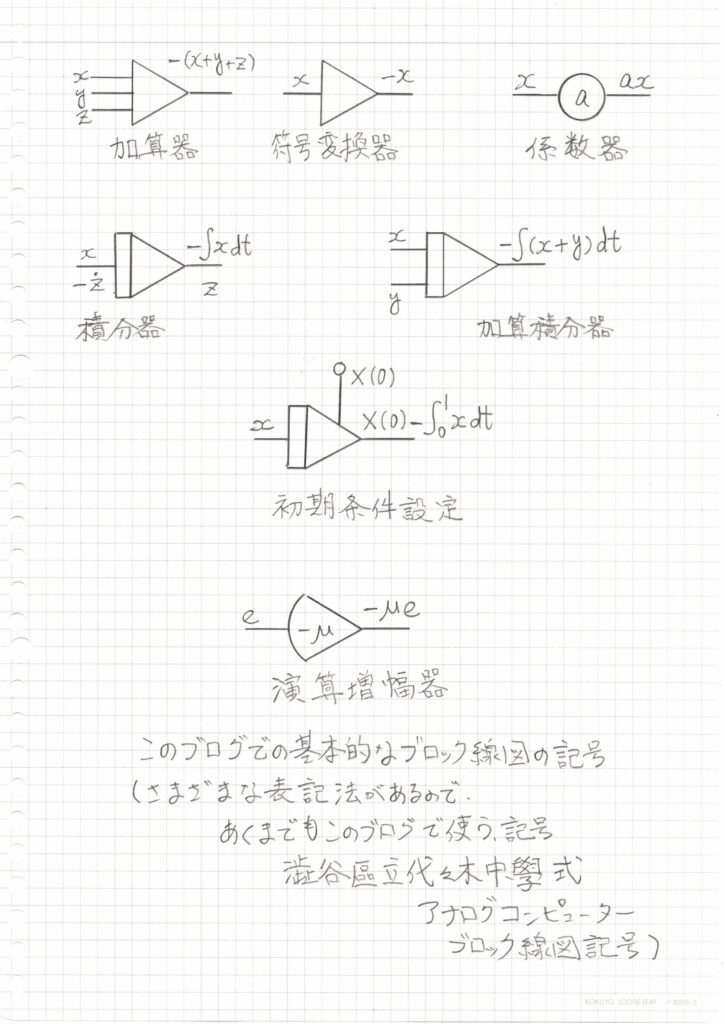
さてアナログコンピュータのプログラミングは通常、ブロック線図というのを書いて検討します。
それには各機能的かたまりの記号の表記法を先に定義しておく必要があります。
だいたい標準的な表記法は決まっていますが、もしかしたら違うかもしれません。
そこできょうの添付図(手書き図)には基本的なブロック線図記号を描いてつけました。
よそ様のアナログコンピュータプログラミングの描き方とほとんど同じだと思います。
でも万が一違うかもしれないので、私のブログで使う表記法を「澁谷區立代々木中學式アナログコンピューターブロック線図記号」略して「代々木式アナコン記号」と名付けます。
あ、これでもまだ長いので「代々アナ式(よよあなしき)」と名付けます。
別に代々木中學の卒業生でなくてもこの表記法を取り入れてかまいません。
もし長崎県福江島ご出身のかたが代々アナ式を使おうとも、江西省上饶职业技术学院のかたが使おうとも全く自由です。
記号表記は手描き図をご覧ください。
加算器、符号変換器、係数器、積分器、加算積分器、初期条件設定の描き方、演算増幅器についての「このブログでの」記号書式をこの図で定義しました。
ところで2つの疑問が頭に浮かんだでしょう?
ひとつは今までたくさん書いてある「過渡現象」とアナログコンピュータの関係は?
そして出力は数値ではなくグラフなのはなぜ?
また積分回路にしろ微分回路に電気の変化を何秒後にどうなっているかですよね。
しかし実際の計算要求需要では「経過時刻について積分する」とか経過の変化とかそういう現象の計算とは限りませんよね。
むしろ時刻ではない要素について積分したり微分する計算は多いでしょう。
でもアナログコンピュータは独立変数を経過時間にたよるのですからアナログコンピュータのプログラミングは独立変数を経過時間にしてしまうような事前準備が必要です。
計算尺をお使いになった経験があれば仮数部の有効数字はたかだか3桁ですからケタが大きく異なる数値が混じっている場合の取捨選択も重要です。
計算の途中で100兆の数字と12の数字が表れて足し算や引き算する場合にもし銀行業務なら「12円ぐらいどうでもいいや」というわけにはいきませんが、水タンクの流量調節弁の自動調整システムならまちがいなく計算基準スケール合わせで12の2桁数字は捨てられるでしょう。
アナログコンピュータのプログラミングではこういうのをスケーリングと言います。
計算尺でも有効数字はn.nn×10の何乗という形にしますから上記12は捨てるでしょう。
でも銀行業務ならすてたらいけません。
さて、今回の手描きの図には積分器はあるのに微分器がありません。
過渡現象では積分回路だけでなく微分回路もたしかにありました。
それなのに微分器がない・・・・・
いったいどうしてでしょう。
これについては昭和30年代に書かれたアナログコンピュータの教科書と昭和40年代になってから書かれたアナログコンピュータの教科書では違う場合がありました。
昭和30年代の教科書には微分器があるものもあったような気がします。
いずれにしてもこのブログの前のほうでは積分器だけでなく微分器も紹介しています。
たぶん(私の勝手な想像では)定電圧装置の性能の問題ではないかと思います。
間違っていたらごめんなさい。
昭和30年代前半ぐらいまで電圧にはわずか(かどうかわかりませんが)一定に見えて結構揺れていたように思います。
そういう揺れをまともに微分してしまうと大きな値になります。
次回からアナログコンピュータの各コンポーネント(○○器 とか 〇〇回路とか)を記号とともに少数使った例を挙げて解説していきます。
(最初はかんたんなものから)









コメント