まず低速型アナログコンピュータ(slow type analog computer)は値段が高い高精度のものがあります。
誤差は0.1%ぐらいだそうです。(昭和30年代 真空管式)
直流増幅器には「ドリフト」と呼ばれる使っているうちに素子の経年変化でだんだん狂ってくる現象があります。
高級品はそのドリフトを修正するような工夫があるらしいです。 くどいようですが私は低速型を使った経験がありません。従ってこのあたりの話は私にはよくわかりません。
あくまでも教科書レベルの知識で書いています。(繰り返し型については使った経験をもとにした思い出話なので記憶違いが無ければ正しい経験話をかけているはずです)
さて低速型はパネルにあいている穴へ接続用ケーブルのバナナチップ端子を突っ込んで演算器どうしを結んでいくプログラミング作業をします。
デジタルコンピュータのプログラミング作業とはずいぶん違います。
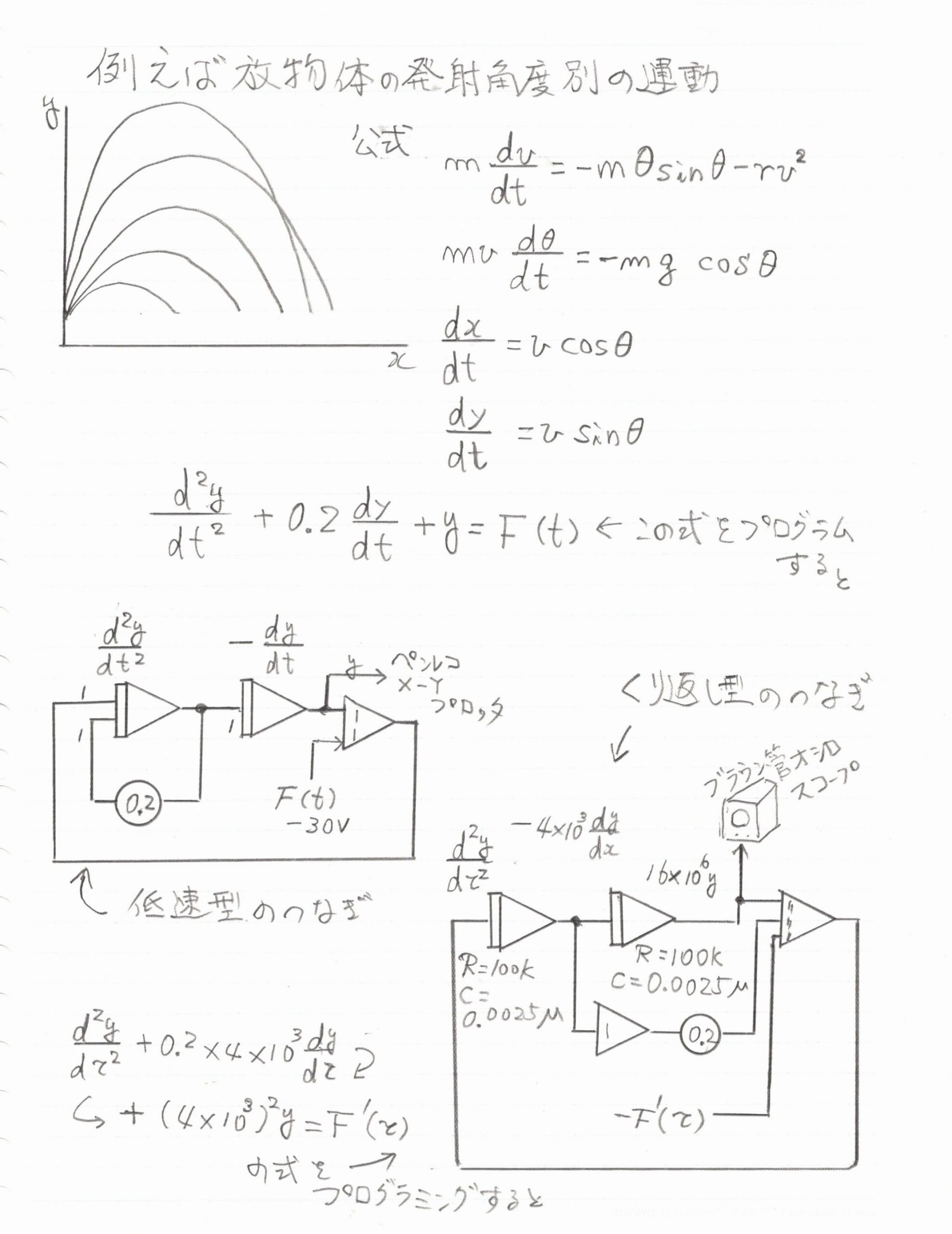
何かプログラミングのネタになりそうなものが無いかなとネットを探していたら「空気抵抗を考慮した放物体の発射角度別の運動」という公式集を見つけました。
この場合、空気抵抗がどうの・・発射角度がどうの・・放物体の運動がどうの・・・とかについてはどうでも良くて、書いてある方程式を素直にアナログコンピュータでプログラミングするときはどうすればいいのかが重要です。
「お客様がこういうプログラムを組んでくれ」とおっしゃたら仕様をうかがってそのまま素直にプログラミングすることが大切です。
お客様のお仕事に首を突っ込んでいたらお客様の機密を知ってしまうことにもなりかねません。
「中身はブラックボックスで、言われた通りに組む」これが大事です。
手描き図の上半分はお客様からのプログラミング仕様指図(さしず)書だと思ってください。
示された公式の意味などわからなくて良いので、提示された微分方程式の・・・
d^2y/dt^2 + 0.2×dy/dt + y = F(t)
という式をプログラミングすれば良いのです。
まん中よりちょっと左下のブロック線図を描くことができれば良いのです。
低速型ですから電圧や電流のレンジが広く、仕様書どうりに組むことができました。
まず各積分器をセット命令で動作状態にします。
プログラミング仕様の式 d^2y/dt^2+0.2×dy/dt+y=F(t)の右辺のF(t)に当たるのが
30Vと決めて(これは決めないと計算ができません。相対的な値です)加算計数器へ与えます。
このF(t)ですが、tが0より大きいときは30Vで、0より小さいときは0Vで、tが0のときはdy/dt=y=0とします。
これをX-Yプロッタで描くと各発射角度ごとの放物線を図の左上のように描いてくれます。
もしペンレコ(ペン記録紙というロールを動かしてくれる装置)で描くと時間の経過に従って紙が動きますから、(時間の経過に従って)ヘビがくねくね這っているみたいな振動グラフになります。
昔、図書館でこれと似たような話が書いてある本を読んだ記憶がありますが、ペンレコの図とX-Yプロッタ装置が描いたグラフが逆に挿図されていました。
結構えらい先生が書いた本で出版社も電気の本をたくさん出版されている権威ある出版社のご本でしたのでびっくりしました。
専門書をお読みになる場合まるごと正しいと思い込んで読むと(まぁたいした話ではありませんけど)単純ミスが意外に多いものですね。
もっともソフトウエアだってバグが無いプログラムなんてこの世にありませんよね。
スマホだってパソコンだって、毎日山のようなアップデートが来ますもんね。
・・・というわけで専門書の中に間違いを見つけると鬼の首でもとったかのようなうれしい気分になれるのですけど、自分だって結構たくさんの誤り記述をしているに違いないので誤りに目くじらをたてるのはやめましょうね。 特に私のブログでは。
次にもうひとつの大分類である繰り返し型アナログコンピュータ(repetitive type analog computer)について書かせていただきます。
原理とか構成する要素(積分器だとか加算計数器だとか・・)の種類は低速型と同じです。
だからブロック線図に描く要素のシンボルも同じかっこうをしています。
何が違うかは昨日投稿しましたように低速型には電磁リレーなどを利用したスイッチがあって演算開始だの停止だのを手でやっていました。
(あくまでも私が書いている話は昭和30年代の思い出話です。 西暦でいえば1950年代後半から1960年代前半までです。あのアジア初開催の最初の東京オリンピックが昭和39年(1964年)でしたから、あれよりも前の時代の話を書いています。
現代の話ではないのでそこはお間違えくださらないようにお願いします。)
繰り返し型の場合は真空管でスイッチングします。
昨日の比較図をご覧いただければ真空管のグリッドへゲート信号を与えていますよね。
ゲートというくらいですから、門を開けたり閉めたりしているわけです。
門が開けばコンデンサに溜まった電気は放電されてその過渡現象を利用して模擬現象を計算しているのです。そのタイミングはゲートの開け閉めタイミングです。
演算増幅器には直流増幅器と交流増幅器を使う場合がありました。
ネットを眺めていたら「直流増幅器とはなんですか?」という質問がありました。
回答は特に問題なかったのですが、最後に付け加えて「オペアンプは直流増幅器である」というひとことが加えられていました。
でも少なくとも昭和30年代の演算増幅器は直流モノもありましたし、交流モノもありました。
まぁいちいちそういうどうでもいいことを見つけて喜んでいるようでは私も末期高齢者としての人格を疑われてしまいますよね。
以後、慎みます。
演算の制御方法が繰り返し型では結構違ってきます。
手描き図のいちばん左下の式を見ていただくと係数がついていますよね。
右下の結線図のように時定数を調整することになります。
繰り返し型では自動的に積分器のコンデンサの電荷を放出させたり蓄電させたりを繰り返すのです。
真空管のグリッド(真空管については後日ちゃんと説明します)の電気がスイッチの役目を果たします。
普通は演算時間とリセット時間が同じ割合で繰り返します。
低速型は積分器のコンデンサにあらかじめ蓄電してから演算に入りますが、繰り返し型では一次積分器の後ろに二次積分器と並列に加算器をつないで演算開始とともにステップ電圧をかけます。
繰り返し型の演算増幅器のゲインは70デシベルくらいです。(低速型はその倍以上です)
それが精度の点で(低速型よりも)劣る原因です。
演算インピーダンスの精度も低速型ほどにする意味がありません。
このあたり低速型のようにしっかりした筐体に納めないでコンデンサや抵抗器を外付けにして臨機応変に自由につないで目的の計算に近づける工夫をするのが腕の見せ所だと東京都立杉並職業訓練所の先生がおっしゃっていました。
(あのころはどういう話だかよくわかりませんでしたが、後年になって中国・上海市でお世話になっているおうちが上海西部の松江区にあったころ、4階のサンルームに泊めていただいていたときに部屋に備え付けてある海尔(ハイアール)社製の空調が全く冷えなくて、メンテ屋さんに来ていただいたことがありました。
そのかたが日本の会社で自動制御機器を開発していた経験をお持ちで、このあたりのことを会話したことがありました。そのかたから詳しく教えていただきました。
低速型でやったd^2y/dt^2+0.2×dy/dt+y=F(t)の式を繰り返し型でやる場合はこのままでは具合が悪いのです。
仮に繰り返し周波数が50ヘルツの場合(1秒間は1000ミリ秒ですから1000÷50=20ミリ秒が1サイクルになります)で演算に必要な時間を10ミリ秒としますと低速型の場合のような時定数では10ミリ秒のあいだに解をだせるかどうかわかりません。
そこで、こういうときは「時間のスケール変換」ということをしなければなりません。
アナログコンピュータは計算したい事柄を電圧とその変化を見る時間とで模擬的に表現するものですから、電圧変化が始まってからひと区切りの過渡現象が終わるまでに時間がかかります。(時間の経過で電圧の変わり具合を見て解を求める計算機なのですから)
たとえばこの下のほうにある繰り返し型ではt=4×10^3τという時変数を考えて方程式を修正します。
dy/dt=dy/dτ×dτ/dt=0.25×10^-3×dy/dτ
d^2y/dt^2=(0.25)^2×10^ – 6×d^2y/dτ^2
もとの式はd^2y/dτ^2+0.2×4×10^3×dy/dτ+(4×10^3)^2y=F´(τ)
コンピュータで千分の1秒で現れる現象はもとの方程式の4秒間に現れるに等しいのです。
右下の図に書き込んであるRやCのパラメータはこのスケール変換された時定数なのです。
低速型アナログコンピュータのほうが、こういう変換をしなくて良いことが多いですし、計算の精度が高いですし、パネルには結線用のリード線を突っ込む穴もあいていますし、良いことづくめみたいな気もします。
でも価格がはるかに高いですし、融通の利かせ方も繰り返し型に比べると厳しいです。
というわけで、低速型と繰り返し型の比較表もつけました。(ほかにも何かあるかもしれませんが、おもいつくままに・・・・)










コメント