皆さんはプラニメーターをご存知ですか？

山登りやハイキングや自転車で山の中を駆け回る人、・・・・・。
昔は地図の上をプラニメーターでこすっていました。
それだけではありません。
複雑な形をした囲いの輪郭をこすって輪郭の内側面積を知るにも便利です。
私は昔、ＪＲ九州（九州旅客鉄道）様へ大型コンピュータを買っていただいたときに博多信号通信区のかたが「レールの断面積が足りているか」などをあれで検査されているのを見ました。
今なら写真撮ってアプリでわかってしまうのでしょうけど。
　アイキャッチ画像は私の中国語の先生が荒崎海岸で岩登りをしている姿です。
プラニメーターの原理を説明するためにアイキャッチ画像に使える山の写真を探したのですけど、山っぽいのが無かったので、私が中国語の先生と荒崎海岸へピクニックへ行ったときの写真を載せてみました。

　プラニメーターはこのブログの最初のころにたびたび登場していただいたイギリスの科学の巨匠、ケルヴィン男爵さんが考案したケルヴィンの積分器の原理を応用しています。
だからアナログコンピュータの一種みたいなものです。
応用につきましてはネットに「機械式計算機の会」というのを見つけたら、プラニメーターのことを書いてありました。
ウィキペディアでプラニメーターのことを読んだらものすごく難しい記述だったので「これがわかる人は果たして何人いるのだろうか？？」と疑問に感じました。
機械式計算機の会のかたも私同様に「これがわかるかたはいらっしゃるのだろうか」とおっしゃっていました。
このブログでケルヴィン男爵さんの積分器で水平円盤の回転軸に平行じゃないのを一度紹介していますよね。
あれと原理は同じです。
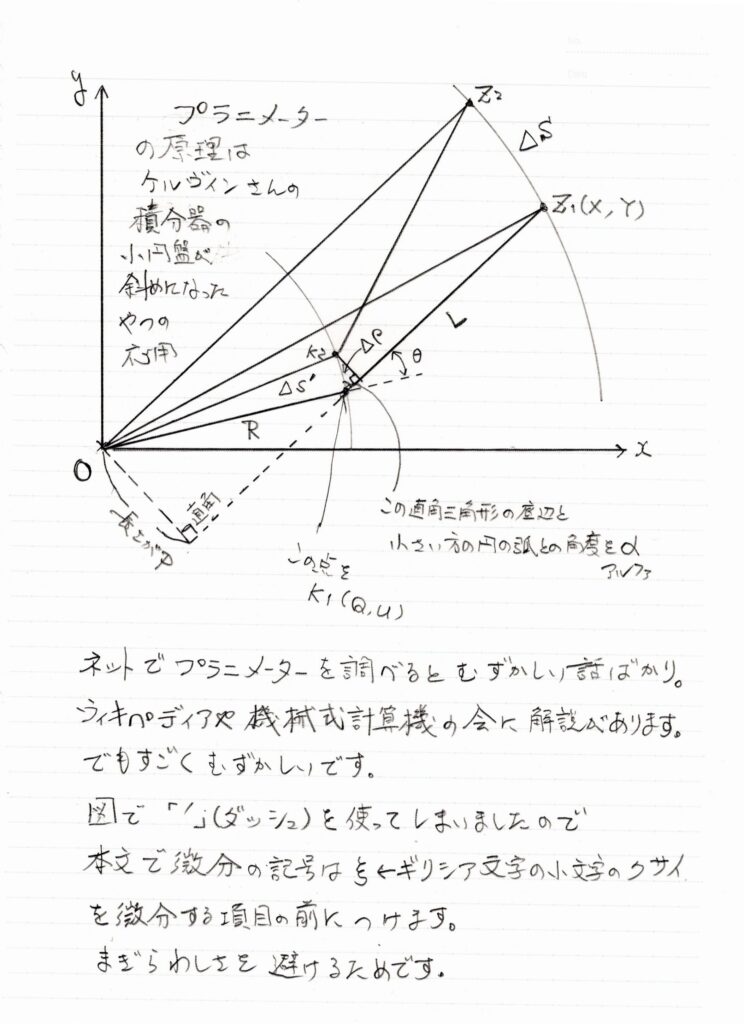
すみませんが、円の一部と線がたくさん書いてある図をご覧ください。
なんで、積分器の説明の最初がプラニメーターなのでしょう。
それは・・・私が代々木中学校の生徒だったころにワンダーフォーゲル部にすごいヤツがいたからです。
そいつは昼休みに校舎の壁面を垂直登り降りしていました。
今なら先生が必死に止めるでしょうが、当時は子供が多かったせいか危険なことをする生徒をいちいち止めるような大人はいませんでした。
高所恐怖症の私はいつもひやひやしてみていました。
山登りをする人が必ず持っていた道具は山岳地図とプラニメーターでした。
そしてこのブログを書くにあたって偶然知ったのはプラニメーターの原理。
このブログの最初のほうで何度も登場するイギリスの巨匠：ケルヴィン男爵さんの積分器と原理がそっくりだということ。
いまでも通販で買えること。
九州に転勤していたころにお客様先の鐡道会社の技術者がレールや橋梁鉄骨の断面積を測定するために使っているのを何度も目撃したことで（わたしにとっては）とても思い出深い道具であることから、原理を調べた知識をいつかご披露したかったことです。
いつもより本文が長くなりますが思い入れが強い道具なのでご容赦ください。

（１）プラニメーター（ケルヴィン男爵さんの積分器の応用例）の原理について
手描きの図でОは円の中心です。
そこから延びる腕ＯＫとＫＺは可動腕です。
腕ＯＫはＯを中心に回転できます。
腕ＫＺはＯＫとＫで連結されていてＫを中心に回転できます。
Ｚがくねくねしているような複雑な輪郭でもたどってその内側の面積を計りたいようなときにたどるための点です。
腕ＯＫの長さをＲ、腕ＫＺの長さをＬとします。
今迄の積分器と同じようにＺが動いている経過時間をτ（タウ）で表します。
τ１の時刻にＺ１に居たという表現を使います。
τ２の時刻にはＺ２に居るというふうに追っていきましょう。
Ｚ１点からＺ２点へ動くときに直線ＯＺ１→ＯＺ２のときにできる弧（Ｚ１→Ｚ２）とＺ１→ＯとＺ２→Ｏとで囲まれた扇型の面積はＺ１の直座標を（Ｘ，Ｙ）と定義しまして、動く時間による微分をξ記号で表しますと・・・
（微分する項目は通常では「´」記号を使いますが本文では図の「´」記号とまぎらわしくなるのでここではギリシヤ文字のξを微分項目記号に使います。以下同様です）
Ｓ＝１／２∫［τ１→τ２］（ＸξＹ－ＹξＸ）dτ
です。
同じようにＫ点（Ｑ,Ｕ）がたどる円弧の軌跡とＯとの腕に囲まれた扇形Ｓ´は
Ｓ´＝１／２∫［τ1→τ2］（Ｑ.ξＵ－ＵξＱ）dτ
ですが、点Ｚと点Ｋの座標間はＸ＝Ｑ＋Ｌcosθです。（cosはコサインです）
Ｌをそのままとして左へ回転する時間について微分すると
ξＸ＝ξＱ－Ｌsinθ×ξθ
ξＹ＝ξＵ＋Ｌcosθ×ξθ
３つの式（Ｘ＝Ｑ＋ＬcosθとξＸ＝ξＱ－Ｌsinθ×ξθとξＹ＝ξＵ＋Ｌcosθ×ξθ）
をＳ＝１／２∫［τ１→τ２］（ＸξＹ－ＹξＸ）dτの式に代入してしまいますと・・・
Ｓ＝Ｓ´＋Ｌ^2／２∫［θ１→θ２］dθ－Ｌ［Ｕcosθ－Ｑsinθ］[θ1→θ2]
    ＋２Ｌ∫［τ１→τ２］（ξＵcosθ－ξＱsinθ）dτ　です。
ところでＬの延長線へＯから直角に線を引きます。
ぶつかったところまでの長さをＰとします。
Ｋの軌跡円弧の微小な長さの弧とΔＳ´の腕ＫＺとの間に小さな三角形ができます。
それを⊿ρとします。
ΔＳ´とＸ軸との間の角度をφと決めますと・・
ｄρ＝dＳ´sin(φ－θ)＝ｄＳ´sinαです。
すると
dＳ´sin(α＋θ)＝dＵ
dＳ´cos(α＋θ)＝Ｑ
dρ＝dＵ×cosθ－dＱ×cosθ－dＱ×sinθ＝（ξＵcosθ－ξＱsinθ）dτ
これらの式を使ってさきほどの・・・
Ｓ＝Ｓ´＋Ｌ^2／２∫［θ１→θ２］dθ－Ｌ［Ｕcosθ－Ｑsinθ］[θ1→θ2]
    ＋２Ｌ∫［τ１→τ２］（ξＵcosθ－ξＱsinθ）dτの式に入れてしまいますと・・
Ｓ＝Ｓ´＋Ｌ^2／２∫[θ1→θ2]dθ－Ｌ[Ｐ][1→2]＋２Ｌ∫[P1→P2]dρ
　＝Ｓ´＋Ｌ^2／２（θ２－θ１）－Ｌ（Ｐ２－Ｐ１）＋２Ｌ∫[P1→P2]ｄρ
です。
ちっともわかり易くなりませんでしたね。　式を少なくしただけでした。すみません。
これではウィキペディアを見ようと、機械式計算機の会のを見ようと私のブログを見ようとも、わかりにくさはほとんど同じということで・・・・